ここではコンピュータでも利用される数値の表現方法を学習しましょう。
数値の表現方法に2進数と16進数と呼ばれる仕組みがあります。
これは2進数なら0と1のみ、16進数なら0から15の数値で数を表現する方法です。
全く分かりません。
難しく考えなくて大丈夫だよ。まずn進数という仕組みを理解しようね。
n進数の概念
身近に使ってる表現に10進数があります。これは1, 2, 3 . . .と数えて10になったら桁が上がる仕組みです。
じゃあ、2進数は2になると桁が上がるの？
そうだよ。n進数のnの数字で桁が上がるんだ。
POINTn進数というのは表現の仕組みであって、理論上はどんな進数でも作ることができます。
例えば12個で1ダースを表現することは12進数です。こういうのをn進法と言います。
2進数 (binary number)
それでは改めて2進数について理解しましょう。冒頭で伝えた通り2進数とは0と1のみで数字を表現する方法です。
ついでに頻繁に使う2進数も見ておきましょう。
| 10進数 | 2進数 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
2進数だと小さな数字も桁が多くて分かりづらいですね。
いい疑問だね。それを解決するのが16進数だよ。
16進数 (hexadecimal)
2進数と仕組みは同じですが、10から15の数値を表現するためにアルファベットが使われます。
具体的にはAからFの文字が使われ、先程の2進数の表に追記すると以下になります。
| 10進数 | 2進数 | 16進数 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
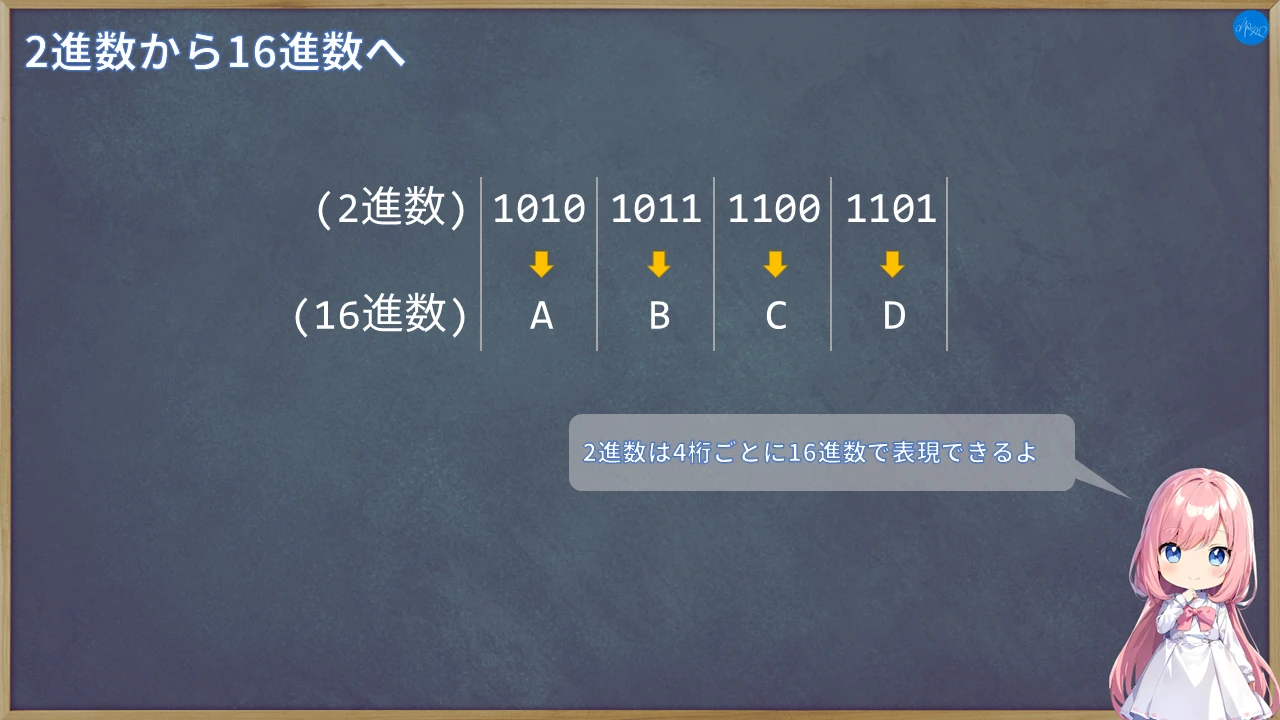
ポイントになるのが2進数の4桁を16進数の1桁で表現できます。これは桁が増えても大丈夫です。
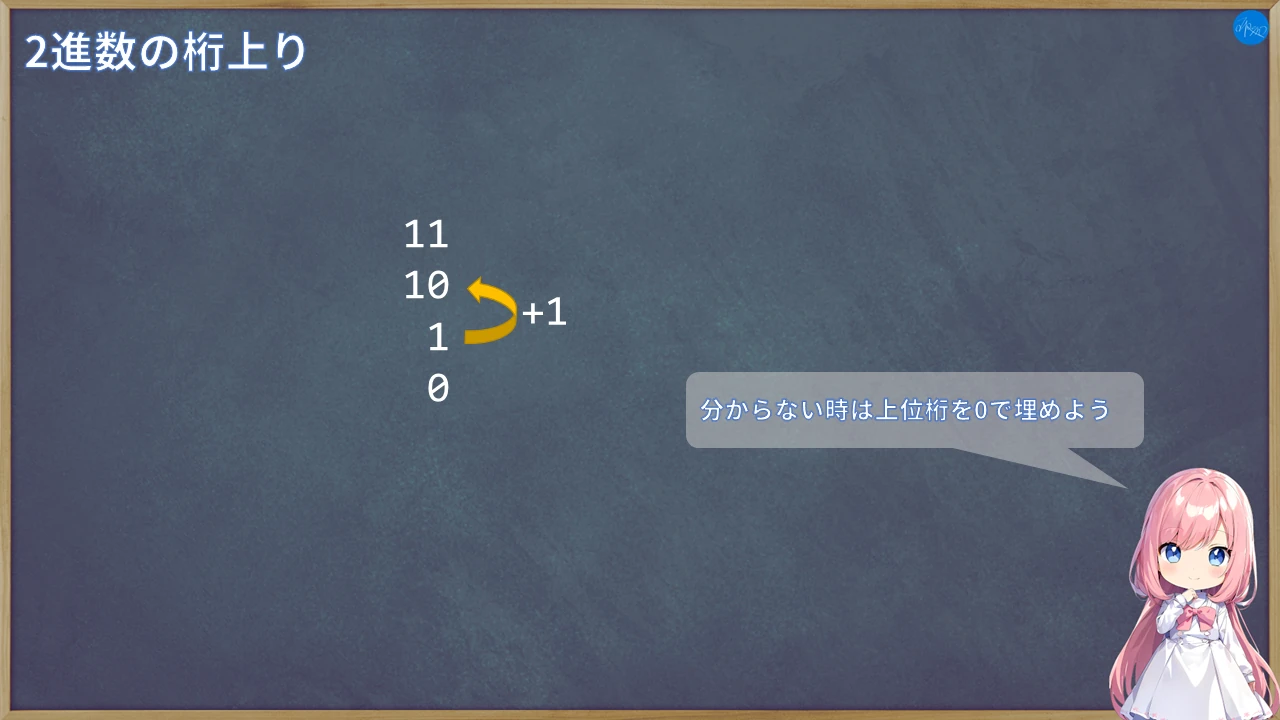
また、桁を揃えるために頭を0埋めすることもあるので、合わせて覚えておきましょう。
0011や00FFみたいに0で埋めて表現する方が圧倒的に多いです。
プレフィックス(prefix)で区別
日本語で言うと接頭辞です。実は先程の表現では問題があります。
記述した数値がn進数のどれか分かりません。
その通り。100と書いても2進数か10進数か区別できないよね。それを解決するためのプレフィックスが用意されてるよ。
仕組みは簡単、数値の頭にn進数を意味する文字を付けます。2進数なら0bを付け、16進数なら0xを付けます。
なお、10進数は日常的に利用されるのでプレフィックスは付けません。
n進数の変換方法
実際に利用するには10進数を2進数や16進数に変換、または10進数に戻す必要があります。
これについては色々方法があるので、別記事で紹介することにしました。
ここでは2進数と16進数と10進数の相互変換を学びます。n進数を理解できてない人は、こちらを参考にしてください。 2進数を10進数に変換する方法 これは全てのn進数に言える理論です。まずn進数の桁上りについて考えてみましょう。n進数において桁が上がると言うことは、小さい位で表現できなくなったので、次の位を+1して、元の位を再度0から始めることです。これは下位桁の数値が全て上位桁に加算されたことを意味します。 何も分かりませんでした。 10進数で考えると簡単だよ。...
あとがき
これ中学か高校の情報で習うらしいけど記憶が無いよ。
どうせ寝てたんじゃないの。
◆ コンピュータサイエンスに関する学習コンテンツ
この記事は参考になりましたか？
コメント