前回の説明でbit演算を解説しました。その中のシフト演算について、伝えるべき特性があるので番外編として紹介します。
別枠の理由は記事が長くなるのと、知っておくべき知識だけど使う必要はないからです。なお、前回の記事は以下です。
コンピュータにはbit単位、つまり0と1だけで演算するbit演算が存在します。それがどんな演算なのか、今回は実用例も交えて学習しましょう。 ちなみにbit単位で演算すると言っても、実際にはbyte単位で処理されます。その場合は複数のbitを計算することになりますが、常に同じ桁同士をbit演算すると覚えれば大丈夫です。 よく分からないけど分かりました。 後に説明するANDとかORの時にこの話を思い出して欲しいな。 論理演算とbitシフト bit演算は、bit単位で...
シフト演算すると何が起きる？
ある数値をシフト演算すると何が起きるのでしょうか。論理シフトを例に考えてみましょう。
ただし、この時に1のbitがはみ出る場合はシフト自体が不可能とルール決めします。
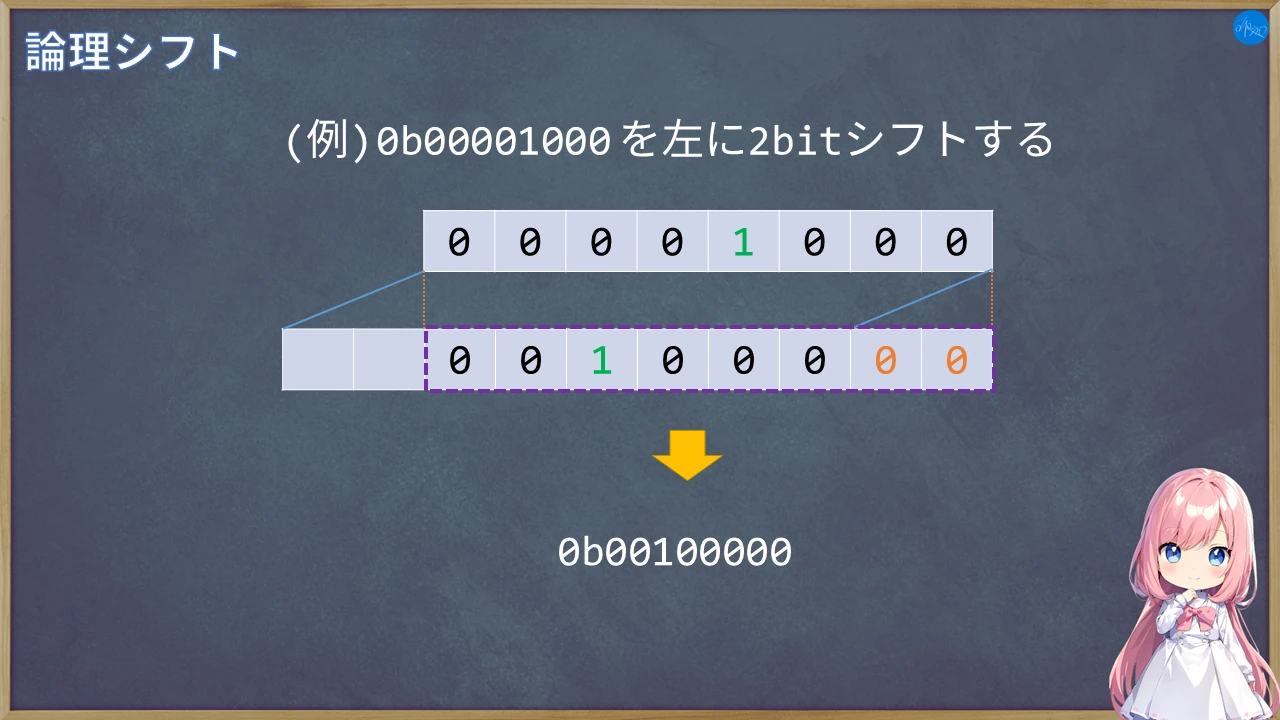
1の場所に注目しよう。何が気が付かない？
そのままの形で桁がズレたように思います。
そう。bit位置を移動するのは桁を移動するのと同じなんだ。
そして2進数で左に1桁ズレるのは2倍、右に1桁ズレると半分になるってことなんだ。
つまり2個シフトしたら2倍の2倍で4倍ですか？
理解が早いね。その値は2のn乗と同じだよ。
はみ出る場合にシフト禁止にしたのは値が壊れるからだよ。見て分かる通り、空きは0で補完されるから理論が成立しないんだ。この値がはみ出て消えることをオーバーフローって言うよ。
POINT値がはみ出ることをオーバーフローと呼ぶ。
算術シフトの場合は？
論理シフトは2倍または半分になりましたが、算術シフトはどうでしょうか？
では、算術シフトの場合でも同じ結果を得られるのか検証してみましょう。
前提として負数の表現は2の補数を使い、オーバーフロー無しで考えます。
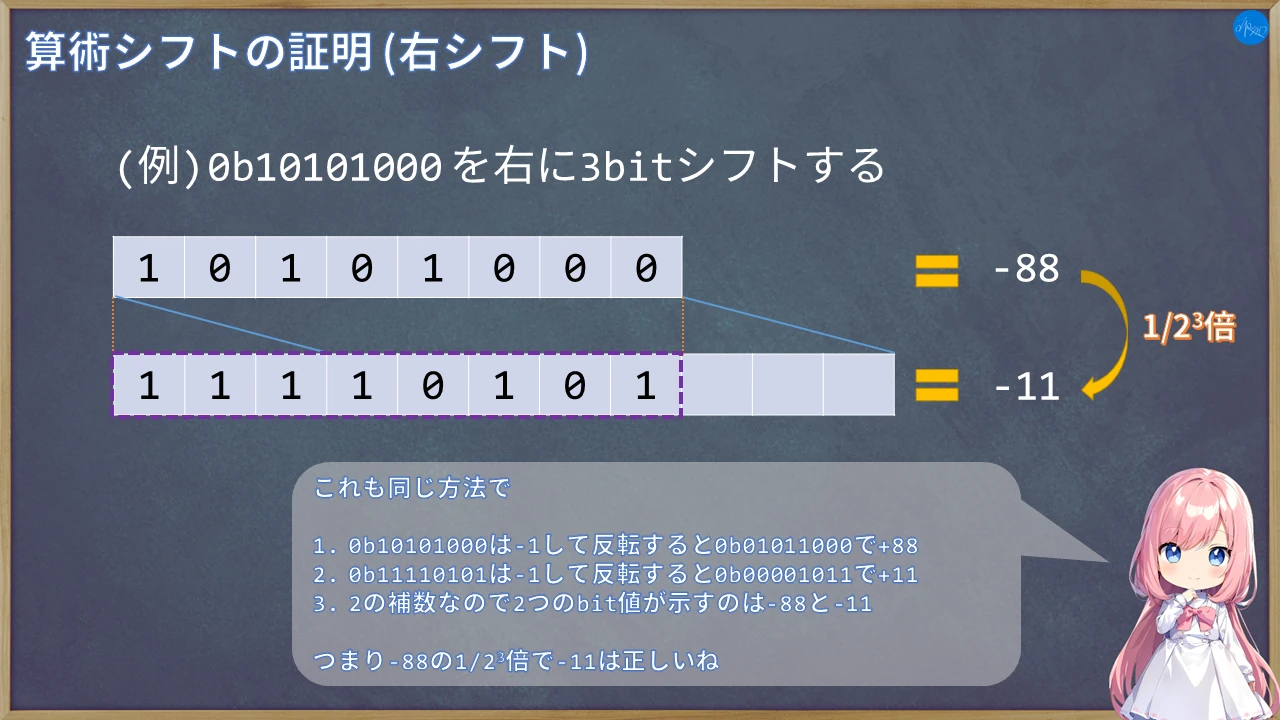
左シフトと右シフトともに正しい結果が得られましたね。よって算術シフトでも問題ありません。
また、負数を例に説明しましたが、正数の場合は符号値0に対して0が保管されるので、論理シフトと同様の結果になります。
先生！ ぱっとみ左シフトがオーバーフローしてるように見えます。
それは2の補数を使ってるからだね。そもそもオーバーフローって言うのは、bit値の上限下限を超える場合に起きるんだ。
今回の場合は8bitだから、-128から+127は表現可能な範囲。この範囲内ならオーバーフローは起きないよ。
あとがき
この特性ってどんな時に使うんですか？
使いません。
えぇ！
ここからはプログラムの話になるから、分からないなら適当に聞いてね。
当然にプログラムは四則演算が記述できます。故にシフト演算で2倍するような記述よりも、x2って書いたほうが見易いコードになります。
さらにプログラムはコンパイルと呼ばれる作業で最適化(高速化)されるのですが、この処理で勝手に変換されるためシフト演算を書くことに意味がないです。
これは実行環境や利用するコンパイラに依存しますが、昨今の事情であればメンテンス性を重視し、普通の書き方をした方が正しい。と僕は思います。
◆ コンピュータサイエンスに関する学習コンテンツ
この記事は参考になりましたか？
コメント